[確認]ボタンをクリックして、１つ１つ確認しましょう。
問題文
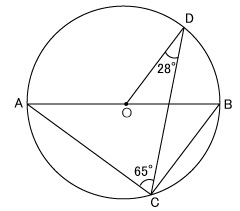
円の直径であり、
2点C、Dは円Oの周上の点である。
このとき、∠ABCの大きさを求めなさい。
解説表示
問題文には書かれていないが、
図から、∠ODC=28°、∠ACD=65°であることがわかる。
問題文の条件から、同じ角度になるところはないか探してみよう。
まず、点Oと点Cを結ぶ補助線を引いてみる。
直線OCも円Oの半径だから、OC=ODである。
故に、△OCDは二等辺三角形となるから、∠OCD=∠ODC=28°である。
同様に、△OACもOA=OCの二等辺三角形だから、
∠OAC=∠OCA=∠ACD-∠OCD=65°-28°=37°となる。
また、線分ABは円Oの直径だから、∠ACB=90°である。
よって、△ABCで、∠ABC=180°-∠ACB-∠BAC=180°-90°-37°=53°である。
図から、∠ODC=28°、∠ACD=65°であることがわかる。
問題文の条件から、同じ角度になるところはないか探してみよう。
まず、点Oと点Cを結ぶ補助線を引いてみる。
直線OCも円Oの半径だから、OC=ODである。
故に、△OCDは二等辺三角形となるから、∠OCD=∠ODC=28°である。
同様に、△OACもOA=OCの二等辺三角形だから、
∠OAC=∠OCA=∠ACD-∠OCD=65°-28°=37°となる。
また、線分ABは円Oの直径だから、∠ACB=90°である。
よって、△ABCで、∠ABC=180°-∠ACB-∠BAC=180°-90°-37°=53°である。
定理の確認
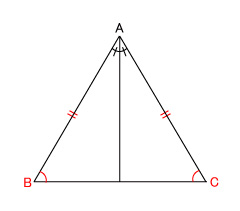二等辺三角形になるための条件定理
三角形の2つの角が等しければ、その三角形は、等しい2つの角を底角とする二等辺三角形である。
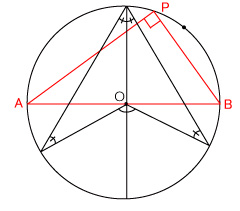円周角の定理定理
1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。
